Mass calibration (metrology) terms explained in plain English.
Air Buoyancy
The buoyant effect of air on an object, acting against the attraction of gravity.
The air is always exerting a lifting effect on an object – on all objects. The magnitude of that lifting effect is a direct function of the density of the air relative to the volume of the object under consideration.
“Normal” air under “perfect” conditions, that is, 20.00 degrees Celsius, atmospheric pressure of 760.5 mm of mercury, and humidity of 50%, has a density of 1.200 mg/cm3.
From a practical standpoint, everything we weigh is surrounded by air, so the convention for expressing the weight, or the mass, of an object, has evolved to express that perceived weight as “mass in air”, or Conventional Mass.
Conventional Mass (Mass in air versus reference density of 8.0 g/cm3)
A hypothetical weighing of a mass in “perfect” air, that is, air of typical composition, at exactly 20.00 degrees C, atmospheric pressure of 760.5 mm of mercury, and a relative humidity of 50%. Under these “perfect” conditions, the density of the air would be 1.2000 mg/cm3.
Since realization of these parameters is a practical impossibility, in a calibration lab the ambient conditions are stabilized to the greatest extent possible, and the temperature, pressure and humidity are carefully measured. From these values the density of the air is calculated, and the results of the calibration are adjusted mathematically to present the result as though the calibration had been conducted in “perfect” conditions.
No discussion of Conventional Mass would be complete without a mention of the 8.0 g/cm3 standard. Stainless steel is the “standard” material from which most high quality laboratory weights are fabricated. Stainless steel has a density of approximately 8 g/cm3, hence the reference. Years ago, brass was the most common material for laboratory weights, and 8.4 g/cm3 was the reference density.
In the real world, the ideal density of 8.0 g/cm3 is seldom realized. Most stainless steel weights have densities of from 7.84 to 7.95 g/cm3, although some of the new weights on the market come very, very close to the ideal density of 8.0 g/cm3.
True Mass (Mass in vacuum)
Contrary to what the name implies, “Mass in Vacuum” is NOT what a weight would weigh in a perfect vacuum, with no air buoyancy effect. The term ‘Mass in Vacuum’ is a misnomer, and causes confusion.
To illustrate the concept of True Mass, consider the following hypothetical example: We have two perfect kilogram weights, each having a Conventional Mass value of exactly 1000.000000 g. The first mass is a calibrated reference mass, made from stainless steel, with an ideal density of 8.0 g/cm3. The second weight is a calibrated mass is also made from stainless steel, but has a commonly seen density of 7.95 g/cm3.
Now let’s consider effect of the air buoyancy on each of the masses:
From basic physics we know that Volume = Mass / Density, so:
The first stainless steel mass has a claimed density (from the manufacturer) of 8.0 g/cm3, accordingly, the volume of this mass is:
1000.000000 divided by 8 = 125.00000000 cm3
The second stainless steel mass has a density from the manufacturer of 7.95 g/cm3, so its volume is:
1000.000000 divided by 7.95 = 125.78616352 cm3
Now – if we could compare these two masses inside a perfect vacuum, there would be NO air buoyancy effect, so we can calculate how much MORE each mass would weigh in a vacuum by multiplying the volume of the mass by the density of “perfect” air:
The 8.0 g/cm3 mass: 125 x 1.200 = 150.00000000 mg
The 7.95 g/cm3 mass: 125.78616352 x 1.200= 150.943396224 mg
We can see that the 7.95 mass weighs more (in a vacuum) than the 8.0 mass by .943396 mg:
150.943396224
-150.000000000
————————-
0.943396224
Accordingly, the True Mass of the 7.95 mass is 1000.000944 (rounding to 6 decimal places).
True Mass, therefore, is not what a weight would weigh in a vacuum, but rather, what it would weigh compared against a reference standard mass (with a known value) on a “perfect” equal arm balance inside a “perfect” vacuum chamber.’
The magnitude of the difference between the Conventional Mass and True Mass is the effect of the air buoyancy on the difference between the volumes of the two masses.
Now we can turn it around and convert back to Conventional Mass:
The formula (from NIST mass calibration procedures) to convert True Mass to Conventional Mass is as follows:
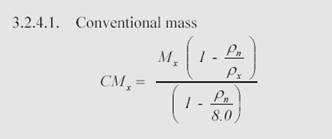
Where:
CMx = Conventional Mass of weight X
Mx = True Mass of weight X
Pn = ‘Normal Air’ density of 1.2 mg/cm3
Px = Density of weight X (7.95)
Work the calculation (1000.000944(1-0.0012/7.95))/(1-0.0012/8) and the result is 1000.000000 (rounded to 6 decimal places).
A well equipped calibration laboratory seeking to undertake high precision measurements of this type, approaches the calibration of mass by creating an environment where the ambient variables are stabilized to the greatest extent possible; then precisely measuring temperature, atmospheric pressure and humidity, calculating the air density from these parameters, and then conducting a matrix of intercomparisons (weighings) between a standard, the weight being tested, and a check standard (a second calibrated mass), using approved procedures and mathematical equations. In the course of the calibration the buoyant effects of the air on the standard, the test weight and the check standard are calculated and compensated for. The laboratory then reports Conventional Mass and True Mass with an appropriate measurement uncertainty attributable to each result.
Think about it:
- If the density of the mass is less than 8.0 g/cm3, its True Mass will be greater than its Conventional Mass.
- The inverse is also true – a mass with a density greater than 8.0 g/cm3 will have a True Mass value smaller than its Conventional Mass value.
- A mass with a density of 8.0 g/cm3 will have exactly the same value for its True Mass and Conventional Mass.
Bottom line: use the Conventional Mass values for standard weight uses – i.e., balance calibration and verification. The True Mass values are typically used only by calibration laboratories, or for reference information.
